矩阵运算

加法

矩阵的加法要求两个矩阵的维度相同，按位置相加。

公式：​ A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}, B = \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix}，则 A + B = \begin{bmatrix} a_{11} + b_{11} & a_{12} + b_{12} \\ a_{21} + b_{21} & a_{22} + b_{22} \end{bmatrix} 。

乘法

矩阵乘法要求第一个矩阵的列数等于第二个矩阵的行数，计算时每个元素是行向量与列向量的点积。

公式：若 ​ A 为 ​ m \times n ，​ B 为 ​ n \times p ，则 ​ C = A \cdot B 是 ​ m \times p ，其中 ​ c_{ij} = \sum_{k=1}^n a_{ik}b_{kj} 。

转置

将矩阵的行和列互换。

公式：若 ​ A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} ，则​ A^T = \begin{bmatrix} a_{11} & a_{21} \\ a_{12} & a_{22} \end{bmatrix} 。

逆矩阵

仅对方阵定义。若 ​ A \cdot A^{-1} = I （单位矩阵），则 ​ A^{-1} 为 ​ A 的逆矩阵。

求法：​ A^{-1} = \frac{1}{\det(A)} \cdot \text{adj}(A) ，其中 ​ \det(A) 为行列式，​ \text{adj}(A) 为伴随矩阵。

行列式

是一个标量，用来判断矩阵是否可逆（若 ​ \det(A) \neq 0 ，矩阵可逆）。

​ 2 \times 2 矩阵：​ \det(A) = a_{11}a_{22} - a_{12}a_{21} 。

特征值与特征向量

对于方阵 ​ A ，若存在非零向量 ​ v 和标量 ​ \lambda ，使得 ​ A \cdot v = \lambda \cdot v ，则 ​ \lambda 为特征值，​ v 为特征向量。

​ A \cdot v = \lambda \cdot v

特征分解 （Eigen Decomposition）

若​ A 可对角化，则 ​ A = P \cdot D \cdot P^{-1} ，其中 ​ P 的列为特征向量，​ D 是特征值构成的对角矩阵。

定义

特征分解是针对方阵​ A 的分解方法，形式为：

​ A = P \cdot \Lambda \cdot P^{-1}

其中：

• ​ \Lambda 是对角矩阵，对角线元素是 ​ A 的特征值。

• ​P是由特征向量组成的矩阵。

条件

矩阵必须是可对角化的（即矩阵的特征向量线性无关）。

对称矩阵必定可对角化，其特征值均为实数。

应用

数据降维：提取最大特征值对应的方向。

稳定性分析： 判断系统矩阵的稳定性（特征值实部决定系统是否收敛）。

动态系统：描述系统行为。

示例（Python实现）

import numpy as np

A = np.array([[4, 1], [1, 3]])

# 特征值与特征向量
eig_vals, eig_vecs = np.linalg.eig(A)

# 还原矩阵
A_reconstructed = eig_vecs @ np.diag(eig_vals) @ np.linalg.inv(eig_vecs)

print("特征值:\n", eig_vals)
print("特征向量:\n", eig_vecs)
print("还原矩阵:\n", A_reconstructed)

这个还原矩阵是什么？还原矩阵是通过矩阵 ​ A 的特征值和特征向量重新计算并近似得到的原始矩阵。让我们分步理解：

特征值分解

对于矩阵 ​ A ，特征值分解表示为：

​ A = Q \Lambda Q^{-1}

其中：

• ​Q 是特征向量组成的矩阵（每列是一个特征向量）
• ​ \Lambda 是特征值组成的对角矩阵。
• ​ Q^{-1} 是 ​ Q 的逆矩阵。

还原矩阵的计算

在代码中，eig_vecs 是 ​ Q ，eig_vals 是特征值的数组，可以用 np.diag(eig_vals) 构造对角矩阵 ​ \Lambda 。然后按照公式 ​ Q \Lambda Q^{-1} 重新计算矩阵 ​ A ，这个重新计算的矩阵就是你的 还原矩阵 A_reconstructed。

为什么叫还原矩阵

理论上，特征值分解后再还原应该等于原始矩阵 ​ A 。

然而，由于计算机在进行浮点运算时的精度限制，A_reconstructed 可能和原始​ A 存在微小的差异。

意义

它验证了特征值分解是否正确。如果 A_reconstructed 与原始​ A 几乎相等，说明特征值分解和还原过程没有问题。

你可以通过以下代码验证误差：

error = np.abs(A - A_reconstructed)
print("误差:\n", error)

如果误差接近零，说明还原矩阵和原始矩阵几乎一致。

主成分分析 （Principal Component Analysis, PCA）

利用协方差矩阵的特征值和特征向量，通过投影最大化数据的方差，实现降维。

流程：计算数据的协方差矩阵，求特征值和特征向量，选择最大特征值对应的特征向量构建新基。

定义

PCA 是一种统计方法，用于从高维数据中提取主要成分，减少维度的同时尽可能保留原数据的方差信息。

流程

标准化数据

计算每个特征的均值并去中心化（减去均值）。

计算协方差矩阵

协方差矩阵 ​ C = \frac{1}{n} X^T X ，描述特征之间的关系。

特征值与特征向量

对协方差矩阵进行特征分解，选择最大特征值对应的特征向量。

投影到新基

用前 ​ k 个特征向量作为新基，将原数据投影到低维空间。

应用

• 数据可视化：在二维或三维空间展示高维数据。
• 特征选择：降低特征冗余。
• 图像压缩：保留图像主要信息，减少存储空间。

示例（Python实现）

from sklearn.decomposition import PCA
import numpy as np

# 示例数据
X = np.array([[2.5, 2.4], [0.5, 0.7], [2.2, 2.9], [1.9, 2.2], [3.1, 3.0]])
print("示例数据:\n", X)


# 去中心化
X_centered = X - np.mean(X, axis=0)
print("去中心化:\n", X_centered)

# 手动计算协方差矩阵和特征分解
cov_matrix = np.cov(X_centered.T)
print("协方差矩阵:\n", cov_matrix)


eig_vals, eig_vecs = np.linalg.eig(cov_matrix)
print("特征值:\n", eig_vals)
print("特征向量:\n", eig_vecs)


# 使用 PCA 方法
pca = PCA(n_components=1)
X_reduced = pca.fit_transform(X)
print("PCA降维结果:\n", X_reduced)

这段代码主要是用 主成分分析（PCA） 方法对二维数据进行降维，并通过手动计算协方差矩阵和特征分解，来展示 PCA 背后的数学原理。下面是详细的解释：

数据准备

X = np.array([[2.5, 2.4], [0.5, 0.7], [2.2, 2.9], [1.9, 2.2], [3.1, 3.0]])

这里定义了一组二维数据 X，每一行代表一个样本点，每一列是一个特征。共 5 个样本，两个特征。

去中心化

X_centered = X - np.mean(X, axis=0)

为了使数据更适合 PCA，需要去中心化，即减去每个特征的均值，使数据的均值为零。
这一步的作用是消除数据中的偏移量，确保协方差矩阵能够反映数据的真正分布。

计算协方差矩阵

cov_matrix = np.cov(X_centered.T)

协方差矩阵描述了各个特征之间的相关性，公式如下：

​ \text{Cov}(X) = \frac{1}{n-1} (X^\top X)

• X_centered.T 是去中心化数据的转置，因为 np.cov 默认要求输入的变量是列向量。
• 输出是一个 ​ 2 \times 2 的矩阵，表示两个特征之间的协方差。

特征分解

eig_vals, eig_vecs = np.linalg.eig(cov_matrix)

对协方差矩阵进行特征值分解，得到特征值（eig_vals）和特征向量（eig_vecs）：

• 特征值：每个特征值表示对应特征向量的方差贡献大小，数值越大，表示该方向上的数据分布越广。
• 特征向量：表示数据的主要方向，指向方差最大的方向。

使用 PCA 降维

pca = PCA(n_components=1)
X_reduced = pca.fit_transform(X)

使用 sklearn 的 PCA 方法对数据进行降维：

• n_components=1 表示将数据从二维降到一维。
• fit_transform 方法会计算数据的主要方向（第一主成分），并将原始数据投影到该方向上。

结果输出

print("协方差矩阵:\n", cov_matrix)
print("特征值:\n", eig_vals)
print("特征向量:\n", eig_vecs)
print("PCA降维结果:\n", X_reduced)

• 协方差矩阵：反映原始数据中两个特征的相关性。
• 特征值：反映每个主成分的重要性（解释的方差比例）。
• 特征向量：表示主成分的方向。
• PCA降维结果：是降维后数据在第一主成分方向上的投影值。

核心思想

• PCA 的目标：找到数据方差最大的方向，作为新的坐标轴（主成分），并对数据进行投影。
• 降维效果：保留数据的主要信息，同时降低维度，便于可视化或加速后续计算。

可视化理解

• 数据原本在二维空间，通过 PCA 降到一维，结果是将数据投影到方差最大的方向上。
• 手动计算协方差矩阵和特征分解的部分，展示了 sklearn PCA 方法的底层原理。

奇异值分解 （Singular Value Decomposition, SVD）

用于降维、矩阵分解。

定义

SVD 将任意矩阵将任意矩阵 ​ A 分解为

​ A = U \cdot \Sigma \cdot V^T

其中：

​ U ：左奇异向量，也叫左奇异向量矩阵，列向量是 ​ AA^T 的特征向量。

​ \Sigma ：奇异值对角矩阵，也叫奇异值对角矩阵，奇异值是​ A 的特征值平方根，其对角线元素是 ​ A 的奇异值。

​ V ：右奇异向量，也叫右奇异向量矩阵，列向量是 ​ A^TA 的特征向量。

性质

• 奇异值分解可以用于任意矩阵（方阵或非方矩阵）。
• 奇异值衡量矩阵的能量分布。

奇异值分解应用

• 矩阵分解：在推荐系统中用于隐含特征提取，图像压缩等。
• 图像处理：图像压缩和去噪。
• 降维：保留最大的 ​ k 个奇异值及对应向量，近似原矩阵。

示例（Python实现）

import numpy as np

A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# SVD 分解
U, Sigma, V_T = np.linalg.svd(A)
print("左奇异向量矩阵 U:\n", U)
print("奇异值对角矩阵 Sigma:\n", Sigma)
print("右奇异向量矩阵 V^T:\n", V_T)

# 奇异值构造对角矩阵
Sigma_full = np.zeros_like(A, dtype=float)
np.fill_diagonal(Sigma_full, Sigma)

# 还原矩阵
A_reconstructed = U @ Sigma_full @ V_T

print("还原矩阵:\n", A_reconstructed)

区别与联系

特征分解

- 只能作用于方阵。
- 分解为特征向量矩阵和特征值对角矩阵。

PCA

- 能作用于任意矩阵。
- 是特征分解的应用之一，利用协方差矩阵的特征值和特征向量实现降维。

SVD

- 能作用于任意矩阵。
- 奇异值与特征值有直接关系，常用于矩阵分解与降维。

通过结合这三种方法，能够从不同角度处理矩阵与高维数据。

线性代数基础应用

用于理解神经网络中的权重矩阵及其操作。

操作示例（Python）

import numpy as np

# 矩阵运算
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# 加法
C_add = A + B

# 乘法
C_mul = np.dot(A, B)

# 转置
C_transpose = A.T

# 逆矩阵
C_inv = np.linalg.inv(A)

# 行列式
det_A = np.linalg.det(A)

# 特征值与特征向量
eig_vals, eig_vecs = np.linalg.eig(A)

# SVD
U, Sigma, V_T = np.linalg.svd(A)

print("加法结果:\n", C_add)
print("乘法结果:\n", C_mul)
print("转置结果:\n", C_transpose)
print("逆矩阵:\n", C_inv)
print("行列式:", det_A)
print("特征值:\n", eig_vals)
print("特征向量:\n", eig_vecs)
print("SVD分解:\n U:\n", U, "\nSigma:\n", Sigma, "\nV_T:\n", V_T)

这个代码覆盖了上述所有内容，可以运行观察结果。

可视化数据_使用 PCA 将 10 维数据降到 2 维

import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns

# 设置中文字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 生成高维数据
np.random.seed(0)
X = np.random.rand(100, 10)

# 输出降维前数据的形状和部分样本
print("降维前数据形状：", X.shape)
print("降维前部分数据：\n", X[:5])  # 输出前 5 行数据

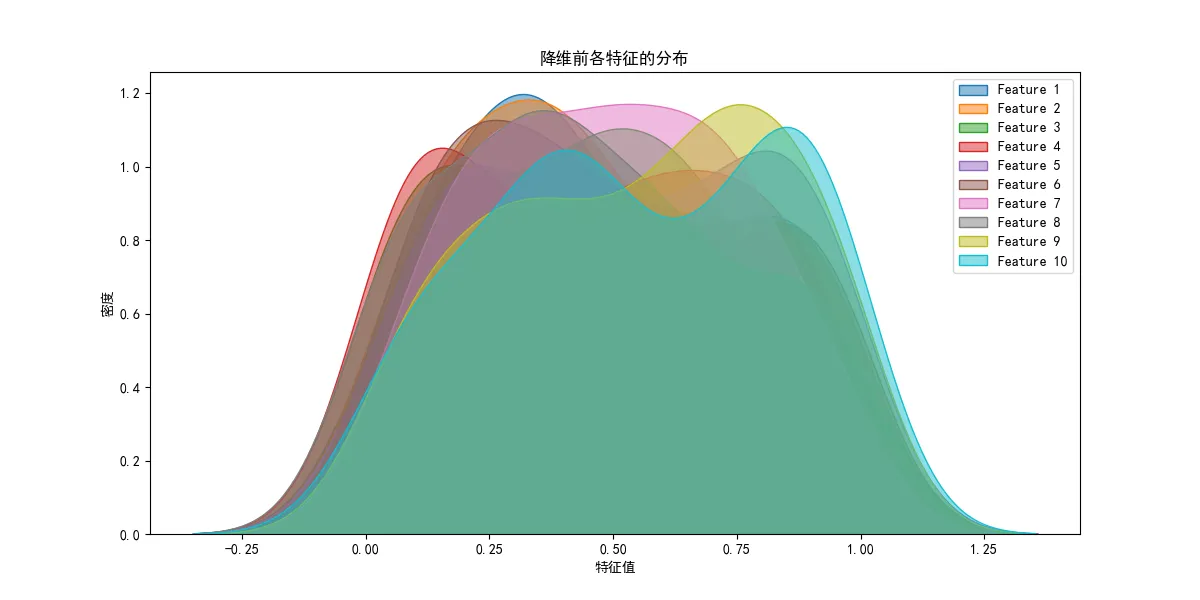
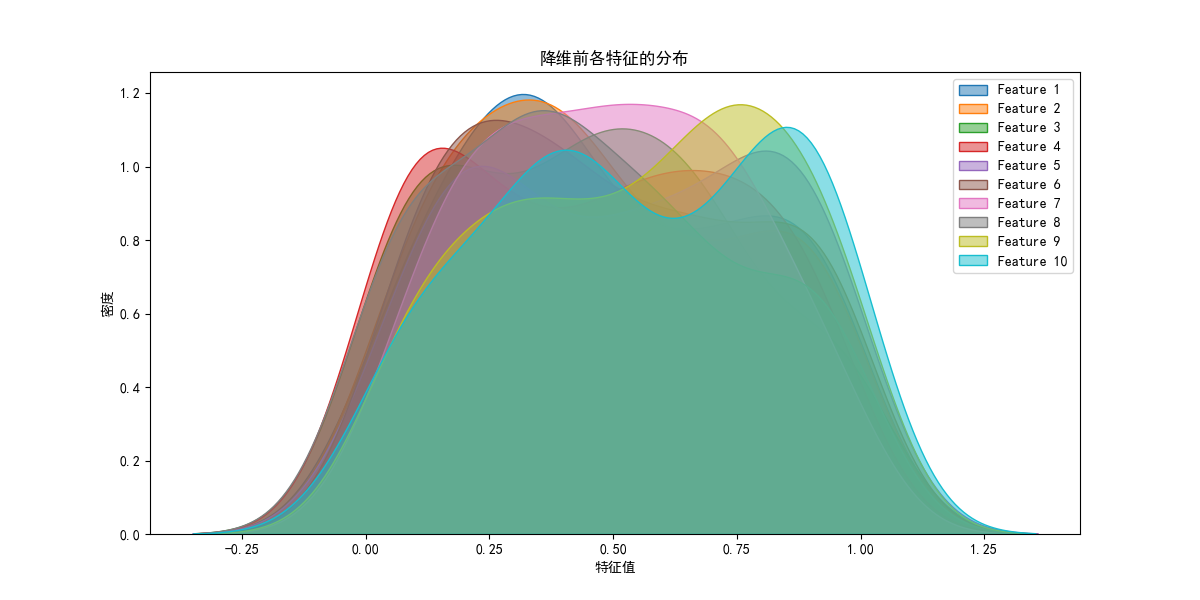
# 绘制高维数据的每个特征分布（使用 Seaborn）
plt.figure(figsize=(12, 6))
for i in range(X.shape[1]):
    sns.kdeplot(X[:, i], label=f'Feature {i+1}', fill=True, alpha=0.5)
plt.title("降维前各特征的分布")
plt.xlabel("特征值")
plt.ylabel("密度")
plt.legend()
plt.show()

# PCA降维
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)

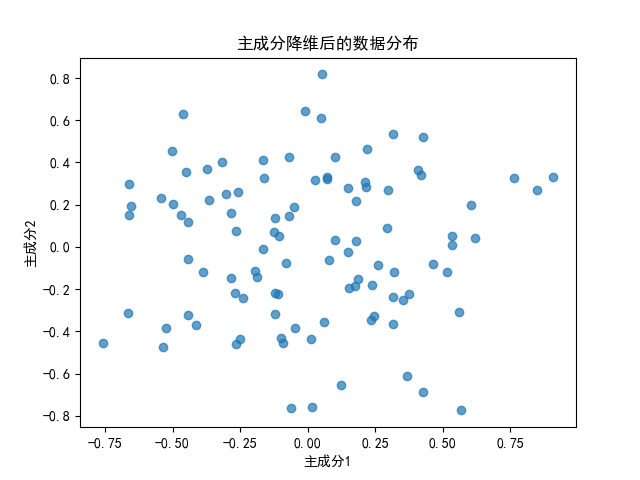
# 可视化降维后的数据
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], alpha=0.7)
plt.title("主成分降维后的数据分布")
plt.xlabel("主成分1")
plt.ylabel("主成分2")
plt.show()

通过 SVD 压缩图片

from skimage import data
from skimage.color import rgb2gray
import matplotlib.pyplot as plt
import numpy as np
import matplotlib

# 设置中文字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 加载图片并转换为灰度
image = rgb2gray(data.astronaut())

# 原图占用空间大小
original_size = image.nbytes

# 奇异值分解 (SVD)
U, Sigma, V_T = np.linalg.svd(image)

# 取前 k 个奇异值重构图像
k = 50
Sigma_k = np.diag(Sigma[:k])
image_reconstructed = U[:, :k] @ Sigma_k @ V_T[:k, :]

# 降维后图像的大小估计
reconstructed_size = (U[:, :k].nbytes + Sigma_k.nbytes + V_T[:k, :].nbytes)

# 调整图布局，增加标题显示空间
fig, ax = plt.subplots(1, 2, figsize=(14, 6))
fig.subplots_adjust(top=0.85)  # 增加顶部空间以显示完整标题

# 原图
ax[0].imshow(image, cmap='gray')
ax[0].set_title(
    f"原图\n大小: {original_size / 1024:.2f} KB\n特点: 全部像素信息，细节完整",
    fontsize=10,
    loc='center'
)
ax[0].axis("off")

# 降维后重构图像
ax[1].imshow(image_reconstructed, cmap='gray')
ax[1].set_title(
    f"SVD降维后重构 (k={k})\n大小: {reconstructed_size / 1024:.2f} KB\n特点: "
    f"高频细节丢失，主要特征保留",
    fontsize=10,
    loc='center'
)
ax[1].axis("off")

# 全局标题（可选）
fig.suptitle("奇异值分解降维效果对比", fontsize=16)

plt.tight_layout()
plt.show()

理解神经网络中的权重矩阵

• 矩阵运算用于计算神经网络的前向传播（加权求和、激活）。
• 特征值分解、SVD 等方法帮助分析权重矩阵的特性，例如降维处理、剪枝等。

神经网络的核心是通过权重矩阵对输入数据进行线性变换和非线性变换，从而逐步提取特征和做出预测。以下是详细的解析：

权重矩阵的作用

权重矩阵是神经网络中的关键参数，用于存储各层神经元之间的连接权重。每个权重代表了一个输入特征对某个神经元输出的重要性。

形状

对于层 ​ l ，假设输入有 ​ n 个神经元，输出有 ​ m 个神经元，则权重矩阵 ​ W 的维度是 ​ m \times n 。

计算

​ z^{(l)} = W^{(l)} \cdot a^{(l-1)} + b^{(l)}

其中：​

• ​W^{(l)} ：第 ​ l 层的权重矩阵。
• ​ a^{(l-1)} ：上一层的激活输出（输入数据）。
• ​ b^{(l)} ：偏置向量，通常与输出神经元个数相同。
• ​ z^{(l)} ：线性变换后的结果。

权重矩阵的含义：

连接强度：

权重矩阵中的每个元素 ​ w_{ij}^{(l)} 表示第​ l-1 层第 ​ i 个神经元与第 ​ l 层第 ​ j 个神经元之间的连接强度。这个值决定了第 ​ i 个神经元在传递信息到第 ​ j 个神经元时的重要性。

学习特征：

在训练过程中，权重矩阵通过梯度下降法不断调整，以学习如何将输入数据映射到正确的输出空间。每一层的权重矩阵都负责抽取不同级别的特征。例如，在图像识别任务中，较低层的权重可能学习到边缘或纹理等基础特征，而较高层的权重可能学习到更复杂的抽象特征，如物体形状或面部特征。

特征空间变换：

    * 权重矩阵 $ W^{(l)} $ 将输入特征空间映射到一个新的特征空间。在每一层，输入特征都会被加权和偏置处理，然后通过激活函数生成输出，这个输出会作为下一层的输入。

直观解释：

低层（如输入层到第一个隐藏层）：这些权重主要学习简单的特征，如边缘、颜色或纹理等。在图像处理的神经网络中，低层权重可以看作是学习如何从原始像素中提取基础信息。

高层（如最后的隐藏层到输出层）：这些权重学习到更复杂的特征，甚至是抽象的概念，如图像中的物体或语句中的语法结构。在深度网络中，随着网络的深入，权重矩阵越来越抽象，能够表示越来越高级的特征。

Q：随着网络的深入，权重矩阵越来越抽象，能够表示越来越高级的特征，这时候权重矩阵应该是越来越小了啊，为什么能够表示越来越高级的特征？

A： 在神经网络中，随着网络的深入，权重矩阵的维度并不会变小，反而通常保持或有时会增加，但其表示的特征却变得越来越抽象和复杂。这是因为神经网络的每一层都对输入数据进行更复杂的非线性变换，因此每层的权重矩阵的作用并不是简单的“维度减少”或者“特征数量减少”，而是将输入映射到不同的特征空间。

1. 为什么深层网络的权重矩阵会变得更复杂

随着网络深度的增加，网络的每一层逐渐从简单特征到复杂特征进行抽象。深层网络的特征表示实际上是通过多次的加权和激活非线性变换，逐步学习到越来越高级的特征，具有更强的表达能力。具体来说：

        + **低层网络**：前几层的神经元学习到的通常是简单的模式或特征，例如在图像任务中，低层的神经元可能学习到边缘、角点、纹理等基本视觉特征。
        + **中层网络**：中间层的神经元开始组合低层学习到的特征，学习到更加抽象的特征，如形状、部件等。
        + **高层网络**：越往深层的神经元，所学习到的特征越抽象，可能涉及到更高层次的概念，如图像中的物体（如人脸、汽车、动物等）或语言中的语法结构等。

这些特征的表示并不是通过“减少维度”来表示的，而是通过多次非线性变换逐渐从低级的特征构建出更为复杂的表示。因此，尽管每层的权重矩阵在维度上可能并没有减少，它所学习到的特征会越来越复杂和高级。

2. 权重矩阵和特征的抽象化

每层的权重矩阵并不意味着每一层只是在“减少”数据的维度，而是通过对输入数据进行一系列加权求和、偏置调整以及激活函数的操作，使得数据可以通过网络传递并在不同层次间逐步提取和重构越来越复杂的特征。

        + **维度与特征的复杂性无关**：网络的每一层可能维持固定的维度（例如从 128128128 个输入特征到 128128128 个输出特征），但它学习到的特征的复杂度却逐层提升。这意味着网络的每一层都在“理解”输入数据的不同层次，而不是仅仅对数据的维度进行简单压缩。
        + **权重矩阵的作用**：权重矩阵在每一层的作用是“映射”输入到一个新的空间，它定义了上一层特征与当前层特征之间的关系。每一层的权重矩阵可以看作是对上一层特征的一个变换，它学习到了如何用上一层的信息来生成更抽象的特征表示。

3. 维度的变化

虽然权重矩阵的维度通常会根据网络结构的需要变化，但它并不意味着深层网络的权重矩阵一定会比浅层网络的矩阵小。在一些网络设计中，可能会保持相同的维度，甚至增加。常见的做法是：

        + **逐层增维或降维**：有些网络设计中，每层的神经元数量（即维度）逐渐增加或减少，例如卷积神经网络（CNN）常常通过池化层减少空间维度，但通过全连接层或更复杂的层提升特征表示能力。
        + **全连接层的权重矩阵**：在全连接层中，网络的每个神经元都有来自前一层每个神经元的输入，因此权重矩阵的维度通常较大。但这些权重矩阵并不是简单地压缩信息，而是通过权重调整从输入数据中提取越来越复杂的特征。

所以，深层神经网络的每层权重矩阵并不会简单地“减小”，它仍然承担着将输入特征空间映射到一个新的特征空间的功能。

随着网络深度的增加，网络能够学习到越来越抽象和复杂的特征，而这并不是通过权重矩阵本身的“维度减少”实现的，而是通过逐层的非线性变换和特征融合实现的。

每一层的权重矩阵将数据从简单特征变换到更复杂的表示，因此神经网络可以处理更高层次、更抽象的任务。

前向传播

前向传播分为两部分：线性变换 和 非线性激活。

加权求和（线性变换）

目的：通过权重矩阵 ​ W 和偏置 ​ b ，对输入数据进行线性组合。

数学公式： ​ z^{(l)} = W^{(l)} \cdot a^{(l-1)} + b^{(l)}

解释：

- 权重矩阵 $ W $将输入数据进行加权。
- 偏置 $ b $用于调整输出，使网络更灵活。

激活函数

目的：引入非线性，使网络能够处理复杂任务（如图像识别、语言理解）。

常见激活函数：

Sigmoid：

​ a = \frac{1}{1 + e^{-z}}

输出范围：​ (0, 1) 。

ReLU：

​ a = \max(0, z)

输出：非负值。

Tanh：

​ a = \frac{e^z - e^{-z}}{e^z + e^{-z}}

输出范围：​ (-1, 1) 。

结合线性变换和激活

在每层中，前向传播的计算步骤如下：

1. 计算线性部分： ​ z^{(l)} = W^{(l)} \cdot a^{(l-1)} + b^{(l)}
2. 应用激活函数： ​ a^{(l)} = \text{Activation}(z^{(l)})

其中 ​ a^{(l)} 是第 ​ l 层的输出，作为下一层的输入。

​ a^{(2)} = \text{Sigmoid}(z^{(2)})

具体示例

假设有一个简单的两层神经网络：

• 输入层：3 个神经元。
• 隐藏层：2 个神经元（权重矩阵 ​ W^{(1)} 大小为 ​ 2 \times 3 ）。
• 输出层：1 个神经元（权重矩阵 ​ W^{(2)} 大小为 ​ 1 \times 2 ）。

输入数据

​ x = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}

隐藏层计算

1. 线性部分： ​ z^{(1)} = W^{(1)} \cdot x + b^{(1)}
2. 激活： ​ a^{(1)} = \text{ReLU}(z^{(1)})

输出层计算

1. 线性部分： ​ z^{(2)} = W^{(2)} \cdot a^{(1)} + b^{(2)}
2. 激活： ​ a^{(2)} = \text{Sigmoid}(z^{(2)})

权重矩阵的意义

特征提取

权重矩阵会自动学习输入数据中有用的特征。例如，在图像处理中，权重可能会学习检测边缘、纹理等。

数据映射

权重矩阵将输入数据映射到更高维度或更低维度的特征空间。

训练中调整

在训练过程中，权重通过反向传播不断更新，以最小化误差。

奇异值分解（SVD）与权重矩阵

SVD 可以帮助我们理解神经网络的权重矩阵：

1. 权重矩阵的分解： 权重矩阵可以被视为由输入到输出的特征转换操作，SVD 可以分解其核心特征。
2. 降维效果： 在低秩近似中，只保留最大的奇异值和对应的奇异向量，类似于神经网络中剪枝的思想。